O MUNDO DAS DIMENSÕES DE GRACELI

 

 

O MUNDO DAS DIMENSÕES DE GRACELI

novembro 16, 2021

 O MUNDO DAS DIMENSÕES DE GRACELI.

ONDE NÃO APENAS O ESPAÇO E O TEMPO SÃO SÃO DIMENSÕES, MAS TAMBÉM TODA FORMA DE ESTRUTURAS, ENERGIAS, CATEGORIAS, FENÔMENOS E ESTADOS FÍSICOS E QUÂNTICO E ESTADOS DE GRACELI. CONFIGURAÇÃO ELETRÔNICA , E OUTTOS

ONDE FORMAM O INFINITO-DIMENSIONAL DE GRACELI.

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

novembro 06, 2021

 TEORIA GRACELI GERAL E UNIFICATÓRIA  do INFINITO-DIMENSIONAL. 

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

outubro 27, 2021

TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL.

ONDE CADA INFINITA PARTÍCULA TEM INFINITAS DIMENSÕES FORMANDO UM SISTEMA GERAL UNIFICATÓRIO COM PADRÕES DE VARIAÇÕES CONFORME AS PARTÍCULA QUE NO CASO PASSAM A REPRESENTAR DIMENSÕES, PADRÕES DE ENERGIAS E E PADRÕES POTENCIAIS DE TRANSFORMAÇÕES, INTERAÇÕES CATEGORIAS FÍSICAS DE GRACELI E OUTROS.

NA TEORIA DAS CORDAS PARTÍCULAS SÃO REPRESNTADAS POR VIBRAÇÕES.

JÁ NA TEORIA GRACELI GERAL E UNIFICATÓRIA DIMENSIONAL. NO CASO SÃO REPRENTADOS POR DIMENSÕES FÍSICAS E QUÍMICA DE GRACELI.

TEORIA FÍSICA DE GRACELI GENERALIZADA ENTRE SDCTIE , TENSORES DE GRACELI, NO :

sistema indeterminístico Graceli ; SISTEMA GRACELI INFINITO-DIMENSIONAL relativismo Graceli.

dimensional graceli.

setembro 20, 2021

 sistema indeterminístico Graceli ;

SISTEMA GRACELI INFINITO-DIMENSIONAL = sdctie graceli, sistema de infinitas dimensões +

SISTEMA DE TENSOR G+ GRACELI , ESTADOS FÍSICOS -QUÍMICO-FENOMÊNICO DE GRACELI CATEGORIAS E Configuração eletrônica dos elementos químicos

SISTEMA GRACELI INFINITO-DIMENSIONAL.

 SISTEMA GRACELI INFINITO-DIMENSIONAL.

COM  ELEMENTOS DO SISTEMA SDCTIE GRACELI, TENSOR G+ GRACELI CAMPOS E ENERGIA, E ENERGIA, E CONFIGURAÇÕES ELETRÔNICAS DOS ELEMENTOS QUÍMICO, E OUTRAS ESTRUTURAS.

ESTADO E NÚMERO QUÂNTICO, NÍVEIS DE ENERGIA DO ÁTOMO, FREQUÊNCIA. E OUTROS.

  TENSOR G+ GRACELI, SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA.

SISTEMA MULTIDIMENSIONAL  GRACELI

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

Configuração eletrônica dos elementos químicos. [parte do sistema Graceli infinito-dimensional].

DENTRO DE UMA CONCEPÇÃO QUE CADA ÁTOMO É FORMADO DE INFINITAs OUTRAS PARTÍCULAS, E COM INFINITAS OUTRAS ENERGIAS, INTERAÇÕES, TRANSFORMAÇÕES, E OUTROS FENÔMENOS, LOGO SE TEM EM CADA ÁTOMO E OU ELEMENTO QUÍMICO INFINITAS OUTRAS DIMENSÕES. COM INFINITAS VARIAÇÕES NAS CATEGORIAS DE GRACELI , QUE  SÃO: OS POTENCIAIS, TIPOS, NÍVEIS, E TEMPO DE AÇÃO ESPECÍFICO  DO FENÔMENO.

ONDE NOS SISTEMAS  DE GRACELI CATEGORIAS,  FENÔMENOS, ESTADOS, ENERGIAS, ESTRUTURAS, E OUTROS SÃO TIPOS E FORMAS DE DIMENSÕES..

FLUXOS ALEATÓRIOS DE ENERGIAS ELÉTRICA,  E FLUXOS DE SALTOS QUÂNTICOS INFINITESIMAIS E INDETERMINADOS.

SENDO QUE VARIAM CONFORME O SISTEMA INFINITO-DIMENSIONAL.

O SISTEMA INFINITO-DIMENSIONAL DE GRACELI, ASSIM, COMO O SISTEMA SDCTIE GRACELI [SISTEMA ENVOLVENDO DIMENSÕES DE GRACELI, E SUAS CATEGORIAS, ESTADOS FÍSICOS E ESTADOS FÍSICOS DE GRACELI, TRANSFORMAÇÕES E INTERAÇÕES], E OS TENSORES DE GRACELI TEM AÇÃO EM TODA A FÍSICA EM TODOS OS SEUS RAMOS E E DIVISÕES, ASSIM, COMO A QUÍMICA E A BIOLOGIA, QUE TODOS ESTES SE FUNDAMENTEM EM ENERGIAS, ONDAS, ESTRUTURAS, CATEGORIAS, ESTADOS, ESPECTROS, DIMENSÕES, E OUTROS.

OU SEJA, DENTRO DE UM SISTEMA GERAL DE GRACELI TODA FÍSICA DAS ESTRTURUAS, ENERGIAS, ONDAS, DIMENSÕES, ESTADOS, E CATEGORIAS. ESTÃO INSERIDOS NESTES SISTEMA DE GRACELI.

dentro de uma concepção que a matéria é infinitésima em termos de tipos e ínfimos diâmetro, logo esta diferenciação faz com que cada ínfima e infinitésima parte tenha ações, transformações, interaçõs, potenciaidades, e outros diferentes de uma das outras. logo se tem infinitas dimensões para cada ínfima e infinitésima parte e tipo.

VEJAMOS;

Autoindutância ou autoindução é o fenômeno no qual o campo eletromagnético gerado pela corrente em um circuito, induz uma tensão no próprio circuito. O componente eletrônico responsável por criar uma Auto-indução significativa em um circuito é o indutor. O indutor é uma bobina feita com o propósito de causar auto-indução. À capacidade auto-indutiva de um indutor, dá-se o nome de Indutância. A unidade de medida da indutância é o henry(H) e ela é frequentemente denotada por L.

Toda corrente elétrica gera um campo magnético, logo, uma corrente ao percorrer um circuito dará origem a um campo magnético que atuará no próprio circuito. Se a corrente for variável, o campo magnético consequentemente irá variar também, ou seja, um circuito percorrido por uma corrente variável induz em si próprio uma força eletromotriz induzida originada pela variação do seu próprio campo magnético. Sua unidade de medida no SI é henry (H).

Onde a f.e.m. neste associada é denominada força eletromotriz autoinduzida, a qual segue a Lei de Faraday. Assim como qualquer outra f.e.m. induzida.

${\displaystyle L=-N\phi b/I}$

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Onde L é a indutância;

N é o número de voltas na bobina;

Φb é o fluxo magnético

I é a corrente.

A F.E.M. Induzida por um indutor é dada pela equação:

$${\displaystyle \varepsilon =-LdI/dt}$$

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Onde ε é a força eletromotriz;

L é a Indutância;

dI/dt é a taxa de variação da corrente elétrica.

Repare que, quando a corrente tentar aumentar, a F.E.M. será negativa e irá se opor a corrente, fazendo com que ela suba aos poucos, na forma de uma assíntota, até seu valor máximo, que é aquele previsto pela lei de Ohm. O contrário acontece quando a corrente tenta diminuir. Esta propriedade dos indutores faz deles excelentes como dispositivos de segurança em aparelhos onde um pico de corrente pode ser prejudicial. Um exemplo de aplicação dos indutores ocorre nas instalações de lâmpadas fluorescentes. Essas lâmpadas são preenchidas com um gás que apresenta um comportamento não-ôhmico. Em determinados instantes, a resistência elétrica da lâmpada pode reduzir muito, demandando uma corrente elétrica muito alta. Essa corrente elétrica pode ser próxima a uma corrente de curto-circuito e causar danos à rede elétrica. Para evitar uma sobrecarga, um Indutor (reator) é adicionado em série à lâmpada. Quando a corrente começa a aumentar, o indutor oferece uma resistência ao aumento da corrente.

Outra característica interessante dos indutores é que a presença de certos materiais pode alterar a indutância de um indutor. Isto faz dos indutores excelentes como sensores. De fato, é comum o uso de Indutores em radares de trânsito e outros dispositivos semelhantes.

O campo eletromagnético é um fenômeno que envolve o campo elétrico e o campo magnético variando no tempo.^[1] As equações de Maxwell constituem basicamente a teoria dos fenômenos eletromagnéticos. No entanto, é importante ressaltar que a Lei de Faraday da indução é um dos importantes princípios do fenômeno.

A Lei de Faraday da indução afirma que o módulo da força eletromotriz induzida em um circuito é diretamente proporcional à taxa temporal de variação do fluxo magnético através do mesmo circuito:^[2]

${\displaystyle \epsilon =-{\frac {d\Phi _{m}}{dt}}}$

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Este sinal negativo que aparece na equação de Faraday é decorrente de outra lei proposta pelo físico Heinrich Lenz, onde a polaridade da força eletromotriz induzida que provoca o aparecimento de uma corrente elétrica gera um fluxo magnético de sentido oposto à variação do mesmo fluxo, através do circuito fechado. Ou seja, com a redução do fluxo magnético no tempo, a corrente induzida cria um campo magnético com mesmo sentido do fluxo; com o aumento do fluxo magnético no tempo, a corrente induzida cria o mesmo campo com sentido oposto ao do fluxo magnético.

Uma experiência que se pode observar, comprovando o campo eletromagnético, é quando se aproxima um ímã de uma espira de um fio condutor ligado a um galvanômetro, notando-se que a agulha indicadora do instrumento desvia a direção. Quando o ímã é afastado, a agulha desvia para uma direção oposta e, havendo esse movimento relativo entre o ímã e a bobina, haverá uma indução de corrente elétrica, criando um campo eletromagnético formado pela interação do campo magnético com um campo elétrico, ou seja, um campo magnético variável no tempo produz um campo elétrico e, da mesma maneira, todo campo elétrico variável no tempo produz um campo magnético. Efeitos como este, não estacionários, constituem basicamente os fenômenos eletromagnéticos.

Índice

• 1Estrutura
  • 1.1Estrutura contínua
  • 1.2Estrutura discreta
• 2Dinâmica
• 3Descrição matemática
• 4Referências

Estrutura

O campo eletromagnético pode ser observado de duas maneiras distintas: como uma estrutura contínua ou como uma estrutura discreta.

Estrutura contínua

Classicamente, campos elétricos e magnéticos foram pensados como sendo produzidos pelo suave movimento de objetos carregados. Por exemplo, cargas oscilantes produzem variações no campo elétrico e magnético que podem ser vistas por uma perspectiva contínua, "suave" e na forma de ondas. Nesse caso, a energia é vista como sendo transferida de maneira contínua através do campo eletromagnético entre dois pontos. Por exemplo, em um rádio transmissor a energia parece ser emitida de forma contínua. Essa visão parece ser útil, mas até certo ponto, pois problemas aparecem quando se trata de altas frequências.^[3]

Estrutura discreta

O campo eletromagnético pode ser descrito de forma mais "fechada". Experimentos revelam que, em certas circunstâncias, a transferência de energia eletromagnética pode ser descrita na forma de pacotes chamados quanta. A relação de Planck liga a energia do fóton E com sua frequência f por meio da equação:^[4]

${\displaystyle E=hf}$ .////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Nessa expressão ${\displaystyle h}$ é a constante de Planck e ${\displaystyle f}$ a frequência do fóton.

Dinâmica

No passado, objetos carregados eletricamente eram pensados como responsáveis pela produção de dois tipos de campos diferentes e associados com suas propriedades de carga. Um campo elétrico é produzido quando uma carga é estacionária em relação ao observador medindo suas propriedades de carga e um campo magnético, assim como um elétrico é produzido quando a carga se move, criando uma corrente elétrica com relação ao observador. Com o passar do tempo, percebeu-se que campo elétrico e magnético são melhor descritos como partes de um todo, o campo eletromagnético. Até 1820, quando o físico dinamarquês Hans Christian Ørsted demonstrou o efeito de uma corrente elétrica em um sistema de bússola com agulha, eletricidade e magnetismo eram tidos até então como fenômenos não relacionados.^[5] Em 1831, Michael Faraday fez a seminal observação de que campos magnéticos variáveis com o tempo podiam induzir correntes elétricas e então, em 1864, James Clerk Maxwell publicou seu famoso artigo A Dynamical Theory of the Electromagnetic Field^[6]

Descrição matemática

Matematicamente, um campo eletromagnético pode ser representado de algumas formas diferentes. A primeira diz que campos elétrico e magnéticos podem ser vistos como campos vetoriais tri-dimensionais. Cada um desses campos possui um valor definido em cada ponto no espaço e tempo e portante, são geralmente escritos como em coordenadas E(x, y, z, t) (campo elétrico) e B(x, y, z, t) (campo magnético).

Se apenas o campo elétrico (E) é diferente de zero e constante no tempo, é dito como sendo um campo eletrostático. De maneira análoga, se apenas o campo magnético (B) é diferente de zero e constante no tempo, é dito como sendo um campo magnetostático. No entanto, se qualquer campo elétrico ou magnético possui uma dependência com o tempo, então ambos os campos devem ser considerados como um campo magnético acoplado usando Equações de Maxwell.^[7]

As ondas eletromagnéticas são uma consequência da formação do campo eletromagnético e se propagam através do vácuo com a velocidade da luz.^[8] Elas são portadoras de energia e, quando se propagam no espaço, podem transferir energia para corpos que se encontram em sua trajetória. Estas ondas são geradas por cargas elétricas que oscilam, ou seja, quando temos campos elétrico e magnético oscilantes e perpendiculares entre si e à direção da propagação da onda, sendo consideradas ondas transversais.^[9]

A amplitude desta onda, segundo Maxwell, esta relacionada por:

${\displaystyle E=c.B}$ , 

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde c é a velocidade da luz.

Um campo elétrico (AO 1945: campo eléctrico) é o campo de força provocado pela ação de cargas elétricas, (elétrons, prótons ou íons) ou por sistemas delas. Cargas elétricas colocadas num campo elétrico estão sujeitas à ação de forças elétricas, de atração e repulsão.

A equação usada para se calcular a intensidade do vetor campo elétrico (E) é dada pela relação entre a força elétrica (F) e a carga de prova (q):

${\displaystyle \mathbf {E} ={\frac {\mathbf {F} }{|q|}}}$

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

O campo elétrico pode ser definido pelo negativo do gradiente do potencial elétrico:

${\displaystyle {\vec {E}}=-{\vec {\nabla }}V}$

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Unidade no Sistema Internacional de Unidades:

${\displaystyle [E]={\frac {N}{C}}\qquad (N/C)}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Onde N é a unidade de força (Newton) e C a unidade de carga (Coulomb).

Índice

• 1História
• 2Vetor campo elétrico
• 3Campo elétrico devido a uma carga elétrica
• 4Campo elétrico uniforme
• 5Linhas de força
• 6Campo elétrico gerado por uma esfera oca condutora
• 7Campo elétrico produzido por cargas pontuais
• 8Lei de Gauss no campo
• 9Campo de um plano
• 10Campo de um fio retilíneo
• 11Campo de uma esfera condutora
• 12Campo elétrico induzido
• 13Propriedades das linhas de campo elétrico
• 14Ver também
• 15Referências
• 16Bibliografia
• 17Ligações externas

História

Os estudos a respeito da eletricidade estática, criadora dos campos elétricos, remontam ao filósofo grego Tales de Mileto no século VI a.C.. O filósofo e estudioso da natureza descreveu o fenômeno que consiste em uma barra de âmbar (seiva petrificada) que atrai pequenos objetos depois de atritada com uma pele de coelho. No cotidiano, é o mesmo que esfregar uma caneta de plástico (material isolante) contra um pano ou o próprio cabelo. Em ambas as situações, o objeto fica eletricamente carregado.

A explicação da força entre partículas através da existência de um campo vem desde a época em que foi desenvolvida a teoria da gravitação universal. A dificuldade em aceitar que uma partícula possa afetar outra partícula distante, sem existir nenhum contato entre elas, foi ultrapassada na física clássica com o conceito do campo de força. No caso da força eletrostática, o campo mediador que transmite a força eletrostática foi designado por éter; a luz seria uma onda que se propaga nesse éter lumínico. No século XIX foram realizadas várias experiências para detectar a presença do éter, sem nenhum sucesso.

No fim do século chegou-se à conclusão de que não existe tal éter. No entanto, o campo elétrico tem existência física, no sentido de que transporta energia e que pode subsistir até após desaparecerem as cargas que o produzem. Na física quântica a interação elétrica é explicada como uma troca de partículas mediadoras da força, que são as mesmas partículas da luz, os fotões. Cada carga lança alguns fotões que são absorvidos pela outra carga; no entanto, neste artigo falaremos sobre a teoria clássica do campo, onde o campo é como um fluido invisível que arrasta as cargas elétricas.

Vetor campo elétrico

Campo elétrico gerado pela carga Q

O campo elétrico em um ponto é uma grandeza vetorial, portanto é representado por um vetor. Para verificarmos a sua presença neste ponto, colocamos neste uma carga de prova positiva. Se esta ficar sujeita a uma força eletrostática, dizemos que a região em que a carga se encontra está sujeita a um campo elétrico. O vetor campo elétrico tem sempre a mesma direção da força a que a carga está sujeita e, no caso da carga ser positiva, o mesmo sentido. Se negativa o oposto. O módulo é calculado da seguinte forma:

${\displaystyle {\vec {E}}={\frac {\vec {F}}{q}}}$ 

O módulo do vetor campo elétrico pode ser definido por:

${\displaystyle E={\frac {F}{q}}}$

Substituindo ${\displaystyle F\Rightarrow E={\frac {k.|Q|}{d^{2}}}}$

${\displaystyle k={\frac {1}{4\pi \varepsilon _{0}}}=8,99\times 10^{9}}$, é a constante de Coulomb ou constante eletrostática do meio e ${\displaystyle \varepsilon _{0}=8,85\times 10^{-12}}$ é a constante de permissividade do vácuo.^[1][2]

Nota-se, por essa expressão, que o campo elétrico gerado por uma carga em um ponto é diretamente proporcional ao seu valor e inversamente proporcional ao quadrado da distância.

Campo elétrico devido a uma carga elétrica

O campo elétrico sempre "nasce" nas cargas positivas (vetor) e "morre" nas cargas negativas. Isso explica o sentido do vetor mencionado acima. Quando duas cargas positivas são colocadas próximas uma da outra, o campo elétrico é de afastamento, gerando uma região entre as duas cargas isenta de campo elétrico. O mesmo ocorre para cargas negativas, com a diferença de o campo elétrico ser de aproximação. Já quando são colocadas próximas uma carga positiva e uma negativa, o campo "nasce" na primeira, e "morre" na segunda.

Na equação: F = k.Q.q/d² , k é a constante eletrostática do meio e não a constante dielétrica.

Campo elétrico uniforme

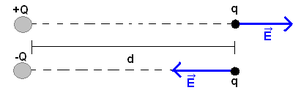
É definido como uma região em que todos os pontos possuem o mesmo vetor campo elétrico em módulo, direção e sentido. Sendo assim, as linhas de força são paralelas e equidistantes.

Para produzir um campo com essas características, basta utilizar duas placas planas e paralelas eletrizadas com cargas de mesmo módulo e sinais opostos. Um capacitor plano de placas paralelas pode ser citado como exemplo de criador de um campo elétrico uniforme.

Linhas de força

As cargas de prova positivas encontram-se em movimento dentro de um campo elétrico. A partir da trajetória dessas cargas, traçam-se linhas que são denominadas linhas de força, que têm as seguintes propriedades:

1. Saem de cargas positivas e entram nas cargas negativas;
2. As linhas são tangenciadas pelo campo elétrico;
3. Duas linhas de força nunca se cruzam;
4. A intensidade do campo elétrico é proporcional à concentração das linhas de força.

Campo elétrico gerado por uma esfera oca condutora

Quando uma esfera está eletrizada, as cargas em excesso repelem-se mutuamente e por isso migram para a superfície externa da esfera, atingindo o equilíbrio eletrostático. Assim, o campo elétrico dentro da esfera (em equilíbrio eletrostático) é nulo.

1. ${\displaystyle E_{i}=0\quad }$ (No interior da Esfera)
2. ${\displaystyle E={\frac {k\cdot Q}{R^{2}}}}$ (superfície exterior próxima da esfera)
3. ${\displaystyle E={\frac {k\cdot Q}{(R+d)^{2}}}}$ (distante da esfera), onde R é o raio da esfera.

Campo elétrico produzido por cargas pontuais

A equação para o módulo do campo produzido por uma carga pontual pode ser escrita de forma vetorial.^[3] Se a carga Q estiver na origem, o resultado obtido é:

${\displaystyle {\vec {E}}={\frac {k\,Q}{r^{2}}}{\vec {e}}_{r}}$

Campos produzidos por duas cargas de 4 nC e 9 nC em alguns pontos (lado esquerdo) e o campo resultante nesses pontos (lado direito)

sendo r a distância até a origem, e ${\displaystyle {\vec {e}}_{r}}$ o vetor unitário que aponta na direção radial, afastando-se da carga.

Se a carga for negativa, a equação anterior continua válida, dando um vetor que aponta no sentido oposto de ${\displaystyle {\vec {e}}_{r}}$ (campo atrativo).

O vetor unitário ${\displaystyle {\vec {e}}_{r}}$ calcula-se dividindo o vetor posição ${\displaystyle {\vec {r}}}$ pelo seu módulo, r.

Se a carga não estiver na origem mas numa posição ${\displaystyle {\vec {r}}_{1}}$ a equação acima pode ser generalizada facilmente, dando o resultado:^[3]

${\displaystyle {\vec {E}}={\frac {k\,Q({\vec {r}}-{\vec {r}}_{1})}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}}}$

O campo produzido por um sistema de cargas pontuais obtém-se somando vetorialmente os campos produzidos por cada uma das cargas.

Por exemplo o lado esquerdo na figura acima à direita mostra os campos produzidos por duas cargas pontuais de 4 nC e 9 nC em alguns pontos. O lado direito mostra o campo resultante, obtido somando vetorialmente os dois campos.

A equação anterior pode ser generalizada para um sistema de n cargas pontuais. Vamos escrever a equação explicitamente, em função das coordenadas cartesianas no plano xy (a generalização para o espaço xyz será evidente).

Se as cargas ${\displaystyle q_{1},q_{2},...,q_{n}}$estiverem nos pontos ${\displaystyle (x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n}),}$ , o resultado é:

${\displaystyle {\vec {E}}=\sum _{i=1}^{n}{\Bigg [}{\frac {k\,q_{i}\,(x-x_{i})}{[(x-x_{i})^{2}+(y-y_{i})^{2}]^{3/2}}}{\Bigg ]}\,{\vec {e}}_{x}+\sum _{i=1}^{n}{\Bigg [}{\frac {k\,q_{i}\,(y-y_{i})}{[(x-x_{i})^{2}+(y-y_{i})^{2}]^{3/2}}}{\Bigg ]}\,{\vec {e}}_{y}}$

Lei de Gauss no campo

O fluxo elétrico através da superfície fechada depende unicamente da carga interna, neste caso q1 + q2.

O fluxo elétrico produzido por várias cargas pontuais, através de uma superfície fechada, é igual à soma dos fluxos produzidos por cada uma das cargas. O fluxo das cargas pontuais que estejam fora da superfície fechada será nulo, e o fluxo das cargas que estejam dentro da superfície será ${\displaystyle 4\,\pi \,k}$ vezes o valor da carga. Por exemplo, no caso da figura abaixo, unicamente as duas cargas ${\displaystyle q_{1}}$ e ${\displaystyle q_{2}}$ produzem fluxo, porque a carga ${\displaystyle q_{3}}$ encontra-se fora da superfície.

O fluxo total é:

${\displaystyle \Phi _{\mathrm {e} }=4\,\pi \,k\left(q_{1}+q_{2}\right)}$

O resultado do exemplo da figura acima pode ser generalizado para qualquer sistema de cargas e qualquer superfície fechada, e é designado de Lei de Gauss:

O fluxo através de qualquer superfície fechada é igual à carga total no interior da superfície, multiplicada por ${\displaystyle 4\,\pi \,k}$

Em termos matemáticos, a lei de Gauss determina que o fluxo elétrico através de qualquer superfície fechada é:

${\displaystyle {\Phi _{\mathrm {e} }=4\,\pi \,k\,q_{\text{int}}}}$

Se a carga total no interior for positiva, o fluxo será positivo, indicando que há linhas de campo a saírem da superfície. Se a carga interna total for negativa, o fluxo é negativo porque há linhas de campo a entrar na superfície.

O fluxo elétrico total à volta de uma carga pontual é diretamente proporcional à carga. Em alguns casos é possível desenhar um número de linhas de campo proporcional à carga, para dar uma ideia mais aproximada do valor do fluxo em diferentes regiões; por exemplo, na figura anterior foram desenhadas 8 linhas de campo a saírem da carga de 4 nC, e 18 linhas a saírem da carga de 9 nC.

A lei de Gauss é muito útil para calcular campos elétricos de sistemas com simetria.

Campo de um plano

Cilindro imaginário usado para calcular o campo do plano.

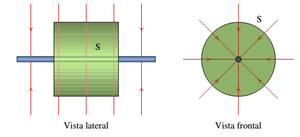
Consideremos um plano, com carga distribuída uniformemente. Visto de lado, o plano aparece como um segmento de reta, e as linhas de campo serão semelhantes às linhas representadas no lado direito da figura ao lado.^[3]

Nas regiões perto do centro do plano, as linhas de campo são aproximadamente paralelas entre si. Quanto maior for o plano, maior será a região onde as linhas são aproximadamente paralelas..^[3]

No caso idealizado de um plano infinito, as linhas serão completamente paralelas e equidistantes, já que a aparência do plano seria a mesma em qualquer ponto.

Para calcular o campo elétrico usando a lei de Gauss, imaginamos um cilindro com as tampas paralelas ao plano, como se mostra na figura.

Nas paredes laterais do cilindro não existe fluxo elétrico, porque o campo é paralelo à superfície. Em cada uma das tampas circulares do cilindro, o campo é perpendicular e, com módulo constante, devido a que todos os pontos na tampa estão à mesma distância do plano.

Assim, o fluxo em cada uma das tampas do cilindro é ,${\displaystyle A\,E}$ , em que A é a área da tampa, e o fluxo total através do cilindro é:^[3]

${\displaystyle \Phi _{\mathrm {e} }=2\,A\,E}$

De acordo com a lei de Gauss, esse fluxo também deverá ser igual a:

${\displaystyle \Phi _{\mathrm {e} }=4\,\pi \,k\,Q}$

Onde Q é a carga na parte do plano que está dentro do cilindro. Igualando as duas últimas equações obtemos o módulo do campo:

${\displaystyle E_{\mathrm {plano} }=2\,\pi \,k\,\sigma }$

Em que ${\displaystyle \sigma }$ é a carga superficial; nomeadamente, carga por unidade de área:

${\displaystyle \sigma ={\frac {Q}{A}}}$

Campo de um fio retilíneo

Linhas de campo de um cilindro com carga distribuída uniformemente, e superfície usada para calcular o campo.

Consideremos um fio retilíneo, muito comprido, com carga distribuída uniformemente. As linhas de campo deverão ser nas direções radiais. Imaginemos uma superfície fechada que é um cilindro de raio R e altura L, com eixo sobre o fio, como mostra a figura abaixo.^[3]

Nas tampas circulares do cilindro o fluxo é nulo, porque o campo é paralelo à superfície; na parede lateral do cilindro, o campo é perpendicular e com módulo constante.^[3]

${\displaystyle \Phi _{\mathrm {e} }=2\,\pi \,R\,L\,E}$

onde E é o módulo do campo à distância R do fio. De acordo com a lei de Gauss, esse fluxo deverá ser também igual a:

${\displaystyle \Phi _{\mathrm {e} }=4\,\pi \,k\,Q}$

onde Q é a carga do fio que está dentro do cilindro S. Igualando as duas equações anteriores, obtemos o módulo do campo:

${\displaystyle {E_{\text{fio}}={\frac {2\,k\,\lambda }{R}}}}$

em que ${\displaystyle \lambda }$ é a carga linear (carga por unidade de comprimento): ${\displaystyle \lambda =Q/L}$

Campo de uma esfera condutora

Numa esfera condutora, com carga Q e raio a, a força repulsiva entre as cargas do mesmo sinal, faz com que as cargas se distribuam em forma uniforme, na superfície da esfera. Existe assim simetria esférica, e as linhas de campo deverão apontar na direção radial..^[3]

Para calcular o campo, imaginamos uma esfera de raio r,concêntrica com a esfera condutora. .^[3] Na superfície dessa esfera, o campo será perpendicular, e com módulo constante E; consequentemente o fluxo será:

${\displaystyle \Phi _{\mathrm {e} }=4\,\pi \,r^{2}\,E}$

Segundo a lei de Gauss, o fluxo através da esfera de raio r será nulo, se ${\displaystyle r<a}$, ou igual a ${\displaystyle 4\,\pi \,k\,Q}$ se ${\displaystyle r>a}$. Portanto, o campo elétrico é nulo, no interior da esfera.

Fora da esfera o campo é:

${\displaystyle E={\frac {k\,Q}{r^{2}}}}$

Que é idêntico ao campo produzido por uma carga Q concentrada no centro da esfera.<.^[3]

Campo elétrico induzido////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde, caso a carga seja puntiforme, ${\displaystyle |{\vec {F}}|={\frac {k.|Q|.|q|}{d^{2}}}}$ (lei de Coulomb)////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

A lei de Coulomb é uma lei experimental^[1] da física que descreve a interação eletrostática entre partículas eletricamente carregadas. Foi formulada e publicada pela primeira vez em 1783 pelo físico francês Charles Augustin de Coulomb e foi essencial para o desenvolvimento do estudo da eletricidade.^[1]

Esta lei estabelece que o módulo da força entre duas cargas elétricas puntiformes (q₁ e q₂) é diretamente proporcional ao produto dos valores absolutos (módulos) das duas cargas e inversamente proporcional ao quadrado da distância r entre eles. Esta força pode ser atrativa ou repulsiva dependendo do sinal das cargas. É atrativa se as cargas tiverem sinais opostos. É repulsiva se as cargas tiverem o mesmo sinal.

Sendo uma lei do inverso do quadrado , a lei é análoga à lei do inverso do quadrado da gravitação universal de Isaac Newton , mas as forças gravitacionais são sempre atrativas, enquanto as forças eletrostáticas podem ser atrativas ou repulsivas.^[2] A lei de Coulomb pode ser usada para derivar a lei de Gauss e vice-versa. No caso de uma única carga pontual estacionária, as duas leis são equivalentes, expressando a mesma lei física de maneiras diferentes.^[3] A lei foi testada extensivamente e as observações confirmaram a lei na escala de 10 ⁻¹⁶ m á 10 ⁸ m.^[4]

Índice

• 1História
• 2Definição
  • 2.1Forma escalar da lei
  • 2.2Forma vetorial da lei
  • 2.3Constante de Coulomb
  • 2.4Limitações
• 3Campos elétricos
• 4Experimento simples para verificar a lei de Coulomb
• 5Notas
• 6Referências

História

Charles-Augustin de Coulomb

Os primeiros investigadores do século 18 que suspeitaram que a força elétrica diminuía com a distância como a força da gravidade (ou seja, como o inverso do quadrado da distância) incluíram Daniel Bernoulli^[5] e Alessandro Volta , ambos medindo a força entre as placas de um capacitor e Franz Aepinus que supôs a lei do inverso do quadrado em 1758.^[6]

Com base em experimentos com esferas eletricamente carregadas, Joseph Priestley, em 1767, foi um dos primeiros a propor que a força elétrica seguia uma lei do inverso do quadrado, semelhante à lei da gravitação universal de Newton.^[7] No entanto, ele não generalizou ou elaborou sobre isso.^[8] Em 1767, ele conjeturou que a força entre as cargas variava como o inverso do quadrado da distância.^[9][10]

Em 1769, o físico escocês John Robison anunciou que, de acordo com suas medições, a força de repulsão entre duas esferas com cargas do mesmo sinal variava em x ^-2,06 .^[11]

No início da década de 1770, a dependência da força entre corpos carregados em relação à distância e à carga já havia sido descoberta, mas não publicada, por Henry Cavendish da Inglaterra.^[12]

Charles Augustin Coulomb foi o primeiro a realizar uma investigação experimental direta da lei de forças.^[13] Em 1785, ele publicou três relatórios sobre eletricidade e magnetismo, onde declarou o que veio a ser conhecido como Lei de Coulomb. Ele utilizou uma balança de torção para estudar as forças de repulsão e atração de partículas carregadas e determinou que a magnitude da força elétrica entre duas cargas pontuais é diretamente proporcional ao produto das cargas e inversamente proporcional ao quadrado da distância entre elas.

A balança de torção consiste em uma barra suspensa em seu meio por uma fibra fina. A fibra atua como uma mola de torção muito fraca. No experimento de Coulomb, a balança de torção era uma haste isolante com uma bola revestida de metal presa a uma extremidade, suspensa por um fio de seda. A bola foi carregada com uma carga conhecida de eletricidade estática, e uma segunda bola carregada da mesma polaridade foi trazida para perto dela. As duas bolas carregadas se repeliam, torcendo a fibra em um determinado ângulo, que podia ser lido em uma escala do instrumento. Ao saber quanta força era necessária para torcer a fibra através de um determinado ângulo, Coulomb foi capaz de calcular a força entre as bolas e deduzir a lei da proporcionalidade do inverso do quadrado.

Definição

Balança de Coulomb

A lei de Coulomb afirma que:

A magnitude das forças eletrostáticas com as quais duas cargas pontuais em repouso interagem é diretamente proporcional ao produto da magnitude de ambas as cargas e inversamente proporcional ao quadrado da distância que as separa.^{[nota 1]}

A força eletrostática atua ao longo da linha reta entre as cargas. Se ambas as cargas possuem o mesmo sinal, a força eletrostática entre elas será de repulsão; se elas possuírem sinais diferentes, a força entre elas será de atração.

A lei de Coulomb também pode ser expressa como uma expressão matemática simples. As formas escalar e vetorial da equação matemática são:

Forma escalar da lei

A forma escalar fornece a magnitude do vetor da força eletrostática ${\displaystyle F}$ entre duas cargas pontuais q₁ e q₂ mas não sua direção. Se ${\displaystyle r}$ é a distância entre as cargas, a magnitude da força é

${\displaystyle |\mathbf {F} |=k_{\text{e}}{|q_{1}q_{2}| \over r^{2}}\qquad }$

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Onde:

• ${\displaystyle k_{e}}$ é a Constante de Coulomb (${\displaystyle k_{e}}$ = 8.9875517873681764×10⁹ N⋅m²⋅C⁻² );
• ${\displaystyle q_{1}}$ e ${\displaystyle q_{2}}$ são as magnitudes sinalizadas das cargas, expressas em Coulomb (C)
• a força eletrostática é dada em Newtons (N )

Forma vetorial da lei

A lei de Coulomb afirma que a força eletrostática ${\displaystyle F}$₁ experimentado por uma carga, q₁ na posição ${\displaystyle r}$₁ nas proximidades de outra carga, q₂ na posição ${\displaystyle r}$₂ no vácuo é igual a:

Diagrama que descreve o mecanismo básico da lei de Coulomb. As cargas iguais se repelem e as cargas opostas se atraem

${\displaystyle \qquad \mathbf {F} _{1}=k_{\text{e}}{\frac {q_{1}q_{2}}{{|\mathbf {r} _{12}|}^{2}}}\mathbf {\widehat {r}} _{12},\qquad }$

Onde:

• o escalar ${\displaystyle r}$ é a distância entre as cargas, dada em metros (m)
• o vetor ${\textstyle r_{12}=r_{1}-r_{2}}$ é a distância vetorial entre as cargas, e ${\textstyle {\widehat {\mathbf {r} }}_{12}={\frac {\mathbf {r_{12}} }{\mathbf {|r_{12}|} }}}$////

  TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

   (um vetor de unidade apontando de ${\textstyle q_{2}}$ a ${\textstyle q_{1}}$).
• a força eletrostática é dada em Newtons (N)

A forma vetorial da lei de Coulomb é simplesmente a definição escalar da lei com a direção dada pelo vetor unitário, ${\displaystyle {\hat {r}}}$₁₂, paralelo com a linha de carga q₂ a carga q₁.^[14] Se ambas as cargas tiverem o mesmo sinal (como cargas), o produto q₁q₂ é positivo e a direção da força sobre q₁ é dado por ${\displaystyle {\hat {r}}}$₁₂ as cargas repelem. Se as cargas tiverem sinais opostos, o produto q₁q₂ é negativo e a direção da força sobre q₁ é -${\displaystyle {\hat {r}}}$₁₂ as cargas se atraem.

A força eletrostática ${\displaystyle F}$2 experimentado por q₂, de acordo com a terceira lei de Newton , é ${\displaystyle F}$2 = ${\displaystyle -F}$1.

No sistema CGS de unidades, que adota cm, g, s como unidades básicas, toma-se ${\displaystyle k=1}$ para interação entre cargas no vácuo, e define-se a unidade de carga como aquela que exerce uma força de 1 dina sobre outra carga idêntica à distância de 1 cm.^[13]

Constante de Coulomb

Ver artigo principal: Constante de Coulomb

A constante de Coulomb é um fator de proporcionalidade que aparece na lei de Coulomb, bem como em outras fórmulas relacionadas à eletricidade. O valor dessa constante depende do meio em que os objetos carregados estão imersos. Denotada, também é chamada de constante de força elétrica ou constante eletrostática,^[15] daí o subscrito ${\displaystyle e}$.

Antes da redefinição das unidades do SI, a constante de Coulomb no vácuo era considerada como tendo um valor exato:

${\displaystyle {\begin{aligned}k_{\text{e}}&={\frac {1}{4\pi \varepsilon _{0}}}={\frac {c_{0}^{2}\mu _{0}}{4\pi }}=c_{0}^{2}\times 10^{-7}\ {H\cdot m}^{-1}\\&=8.987\,551\,787\,368\,176\,4\times 10^{9}\ {N\cdot m^{2}\cdot C}^{-2}.\end{aligned}}}$

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Desde a redefinição,^[16][17] a constante de Coulomb não é mais exatamente definida e está sujeita ao erro de medição. Conforme calculado a partir dos valores recomendados do CODATA 2018, a constante de Coulomb é^[18]

${\displaystyle k_{\text{e}}=8.987\,551\,792\,3\,(14)\times 10^{9}\ {N\cdot m^{2}\cdot C}^{-2}}$

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Em unidades Gaussianas e unidades Lorentz-Heaviside , que são ambos sistemas de unidades CGS , a constante tem diferentes valores adimensionais .

Em unidades electrostáticas ou unidades gaussianas a unidade de carga ( ESU ou statcoulomb ) é definida de tal modo que a constante de Coulomb desaparece, uma vez que tem o valor de um e torna-se adimensional.

${\displaystyle k_{\text{e}}=1}$ (Unidades gaussianas).

Em unidades de Lorentz-Heaviside, também chamadas de unidades racionalizadas , a constante de Coulomb é adimensional e é igual a:

${\displaystyle k_{\text{e}}={\frac {1}{4\pi }}}$ (Unidades Lorentz-Heaviside)

As unidades gaussianas são mais adequadas para problemas microscópicos, como a eletrodinâmica de partículas individuais eletricamente carregadas.^[19] As unidades SI são mais convenientes para fenômenos práticos de grande escala, como aplicações de engenharia.^[20]

Limitações

Existem três condições a serem cumpridas para a validade da lei de Coulomb:^[21]

1. As cargas devem ter uma distribuição esfericamente simétrica (por exemplo, cargas pontuais ou uma esfera de metal carregada).
2. As cargas não devem se sobrepor (por exemplo, devem ser cargas pontuais distintas).
3. As cargas devem ser estacionárias uma em relação à outra.

A última delas é conhecida como aproximação eletrostática . Quando o movimento ocorre, a teoria da relatividade de Einstein deve ser levada em consideração, e um resultado, é introduzido um fator extra, o que altera a força produzida sobre os dois objetos. Essa parte extra da força é chamada de força magnética e é descrita por campos magnéticos. Para movimentos lentos, a força magnética é mínima e a lei de Coulomb ainda pode ser considerada aproximadamente correta, mas quando as cargas estão se movendo mais rapidamente em relação umas às outras, todas as regras eletrodinâmicas (incorporando a força magnética) devem ser consideradas.^[22]

Campos elétricos

As forças de campo podem agir através do espaço, produzindo um efeito mesmo quando não ocorre contato físico na interação entre os objetos. O campo gravitacional ${\displaystyle {\vec {g}}}$ em um ponto no espaço devido a uma partícula de origem como sendo igual à força gravitacional ${\displaystyle {\vec {F}}}$_g agindo sobre uma partícula teste de massa m dividida pela massa: ${\displaystyle {\vec {g}}={\vec {Fg}}/m}$. O conceito de campo foi desenvolvido por Michael Faraday (1791-1867) no contexto das forças elétricas. Diz-se que um campo elétrico existe na região de espaço em torno de um objeto carregado, a carga fonte. Quando outro objeto carregado – a carga teste – entra neste campo elétrico, uma força elétrica atua sobre ele.

Define-se campo elétrico devido à carga fonte no local da carga teste como sendo a força elétrica sobre a carga teste por unidade de carga, ou, mais especificamente, o vetor campo elétrico ${\displaystyle {\vec {E}}}$ num ponto no espaço é definido como força elétrica ${\displaystyle {\vec {F}}}$ agindo sobre uma carga teste positiva q0 colocada nesse ponto dividida pela carga teste:

${\displaystyle {\vec {E}}={\frac {\vec {Fe}}{q0}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

• O vetor ${\displaystyle {\vec {E}}}$ tem unidades no SI de newtons por coulomb (N/C).

Observe também que a existência de um campo elétrico é uma propriedade de sua fonte; a presença da carga teste não é necessária para o campo existir. A carga teste funciona como um detector do campo elétrico: um campo elétrico existe em um ponto se uma carga teste nesse momento experimenta uma força elétrica. Uma vez que o campo elétrico é conhecido em algum momento, a força sobre qualquer partícula com carga q colocada nesse ponto pode ser calculada a partir de um rearranjo:

${\displaystyle {\vec {Fe}}=q{\vec {E}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Uma vez que a força elétrica sobre uma partícula é avaliada, o seu movimento pode ser determinado a partir do modelo de partícula sob força resultante ou o modelo da partícula em equilíbrio (a força elétrica pode ter que ser combinada com as outras forças que atuam sobre a partícula).^[23]

Experimento simples para verificar a lei de Coulomb

Experimento para verificar a lei de Coulomb

É possível verificar a lei de Coulomb com um experimento simples. Considere duas pequenas esferas de massa me carga de mesmo sinal ${\displaystyle q}$, penduradas em duas cordas de massa desprezível e de comprimento ${\displaystyle l}$. As forças que atuam em cada esfera são três: o peso ${\displaystyle mg}$, a tensão da corda ${\displaystyle \mathbf {T} }$ e a força elétrica ${\displaystyle \mathbf {F} }$.

No estado de equilíbrio:

${\displaystyle \mathbf {T} \sin \theta _{1}=\mathbf {F} _{1}}$

//// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

(1)

${\displaystyle \mathbf {T} \cos \theta _{1}=mg}$

//// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

(2)

Dividindo (1) por (2):

${\displaystyle {\frac {\sin \theta _{1}}{\cos \theta _{1}}}={\frac {F_{1}}{mg}}\Rightarrow F_{1}=mg\tan \theta _{1}}$

//// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

(3)

Sendo ${\displaystyle \mathbf {L} _{1}}$ a distância entre as esferas carregadas; a força de repulsão entre elas ${\displaystyle \mathbf {F} _{1}}$, assumindo que a lei de Coulomb está correta, é igual a

${\displaystyle F_{1}={\frac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}}$

//// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

(Lei de Coulomb)

então:

${\displaystyle {\frac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}=mg\tan \theta _{1}\,\!}$

//// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

(4)

Se agora descarregamos uma das esferas, e a colocamos em contato com a esfera carregada, cada uma delas adquire uma carga ${\textstyle {\frac {q}{2}}}$. No estado de equilíbrio, a distância entre as cargas será ${\textstyle \mathbf {L} _{2}<\mathbf {L} _{1}}$ e a força repulsiva entre elas será

${\displaystyle F_{2}={\frac {{({\frac {q}{2}})}^{2}}{4\pi \varepsilon _{0}L_{2}^{2}}}={\frac {\frac {q^{2}}{4}}{4\pi \varepsilon _{0}L_{2}^{2}}}\,\!}$

//// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

(5)

Sabemos que ${\displaystyle \mathbf {F} _{2}=mg\tan \theta _{2}}$ e:

${\displaystyle {\frac {\frac {q^{2}}{4}}{4\pi \varepsilon _{0}L_{2}^{2}}}=mg\tan \theta _{2}}$

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Dividindo (4) por (5), obtemos:

${\displaystyle {\frac {\left({\cfrac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}\right)}{\left({\cfrac {\frac {q^{2}}{4}}{4\pi \varepsilon _{0}L_{2}^{2}}}\right)}}={\frac {mg\tan \theta _{1}}{mg\tan \theta _{2}}}\Rightarrow 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}={\frac {\tan \theta _{1}}{\tan \theta _{2}}}}$

//// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

(6)

Medindo os ângulos ${\displaystyle \theta _{1}}$ e ${\displaystyle \theta _{2}}$ e a distância entre as cargas ${\displaystyle \mathbf {L} _{1}}$ e ${\displaystyle \mathbf {L} _{2}}$ é suficiente para verificar se a igualdade é verdadeira levando em consideração o erro experimental. Na prática, os ângulos podem ser difíceis de medir, portanto, se o comprimento das cordas for suficientemente grande, os ângulos serão pequenos o suficiente para fazer a seguinte aproximação:

${\displaystyle \tan \theta \approx \sin \theta ={\frac {\frac {L}{2}}{\ell }}={\frac {L}{2\ell }}\Rightarrow {\frac {\tan \theta _{1}}{\tan \theta _{2}}}\approx {\frac {\frac {L_{1}}{2\ell }}{\frac {L_{2}}{2\ell }}}}$

//// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

(7)

Usando essa aproximação, a relação (6) se torna uma expressão muito mais simples:

${\displaystyle {\frac {\frac {L_{1}}{2\ell }}{\frac {L_{2}}{2\ell }}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Rightarrow \,\!}$ ${\displaystyle {\frac {L_{1}}{L_{2}}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Rightarrow {\frac {L_{1}}{L_{2}}}\approx {\sqrt[{3}]{4}}\,\!}$

//// TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

(8)

Dessa forma, a verificação se limita a medir a distância entre as cargas e verificar se a divisão se aproxima do valor teórico.

Potencial elétrico é a capacidade que um corpo energizado tem de realizar trabalho, ou seja, atrair ou repelir outras cargas elétricas. Com relação a um campo elétrico, interessa-nos a capacidade de realizar trabalho, associada ao campo em si, independentemente do valor da carga q colocada num ponto desse campo. Para medir essa capacidade, utiliza-se a grandeza potencial elétrico.

Para obter o potencial elétrico de um ponto, coloca-se nele uma carga de prova q e mede-se a energia potencial adquirida por ela. Essa energia potencial é proporcional ao valor de q. Portanto, o quociente entre a energia potencial e a carga é constante. Esse quociente chama-se potencial elétrico do ponto. Ele pode ser calculado pela expressão:

${\displaystyle V={\frac {E_{p}}{q}}\,}$ , onde////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

• ${\displaystyle V\,}$ é o potencial elétrico,
• ${\displaystyle E_{p}\,}$ a energia potencial elétrica
• ${\displaystyle q\,}$ a carga.

A unidade no SI é J/C = V (volt)

Portanto, quando se fala que o potencial elétrico de um ponto L é V_L = 10 V, entende-se que este ponto consegue dotar de 10J de energia cada unidade de carga de 1C. Se a carga elétrica for 3C por exemplo, ela será dotada de uma energia de 30J, obedecendo à proporção. Vale lembrar que é preciso adotar um referencial para tal potencial elétrico. Ele é uma região que se encontra muito distante da carga, teoricamente localizado no infinito.

Índice

• 1História
• 2Potencial elétrico devido a uma carga puntiforme
• 3Superfície equipotencial
• 4Potencial elétrico no eletromagnetismo
  • 4.1Pontos críticos do potencial
• 5Potencial e energia eletrostática
• 6Potencial e campo nos condutores
• 7Potencial de uma esfera condutora
• 8Potencial eletrostático
  • 8.1História
  • 8.2Potencial eletrostático e campo elétrico
  • 8.3Potencial devido a cargas pontuais
  • 8.4Variáveis vetoriais
• 9Ver também
• 10Referências

História

Uma forma simples de sentir o efeito da corrente elétrica consiste em colocar uma colher por baixo da língua e um pedaço de folha de alumínio por cima. Quando se junta a folha de alumínio à colher, sente-se um sabor amargo na língua, produzido pela passagem de cargas elétricas através da língua. Esse fenómeno foi descoberto por Alessandro Volta, no fim do século XVIII. É importante que o metal da folha seja diferente do metal da colher; as colheres são geralmente feitas de aço ou de prata. Na nossa língua existem iões positivos e negativos; um dos metais terá uma maior tendência a atrair os iões negativos e no outro metal os iões positivos serão atraídos, criando um fluxo de cargas através dos dois metais. Volta reparou que o mesmo efeito podia ser obtido colocando dois metais diferentes, dentro de um líquido com uma solução química. Algumas combinações de metais produziam melhores resultados. Conseguiu intensificar mais o efeito colocando alternadamente vários discos de cobre e de zinco, separados por discos de papel humedecidos com água salgada; assim construiu a primeira pilha.

Potencial elétrico devido a uma carga puntiforme

Para calcular o potencial elétrico devido a uma carga puntiforme usa-se a fórmula:

${\displaystyle V={\frac {K\,Q}{d}}}$, sendo////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

• ${\displaystyle d\,}$ em metros,
• ${\displaystyle K\,}$ é a constante dielétrica do meio e
• ${\displaystyle Q\,}$ a carga geradora.

Como o potencial é uma grandeza escalar, o potencial gerado por várias cargas é a soma algébrica (usa-se o sinal) dos potenciais gerados por cada uma delas como se estivessem sozinhas:

${\displaystyle V_{L}={\frac {K\,Q_{1}}{d_{1}}}+{\frac {K\,Q_{2}}{d_{2}}}+{\frac {K\,Q_{3}}{d_{3}}}+{\frac {K\,Q_{4}}{d_{4}}}+{\frac {K\,Q_{5}}{d_{5}}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

• 
 
• 

  Potencial elétrico resultante.

Superfície equipotencial

Superfície equipotencial

Quando uma carga puntiforme está isolada no espaço, ela gera um campo elétrico em sua volta. Qualquer ponto que estiver a uma mesma distância dessa carga possuirá o mesmo potencial elétrico. Portanto, aparece ai uma superfície equipotencial esférica. Podemos também encontrar superfícies equipotenciais no campo elétrico uniforme, onde as linhas de força são paralelas e equidistantes. Nesse caso, as superfícies equipotenciais localizam-se perpendicularmente às linhas de força (mesma distância do referencial). O potencial elétrico e distância são inversamente proporcionais, portanto o gráfico cartesiano V x d é uma assíntota.

Nota-se que, percorrendo uma linha de força no seu sentido, encontramos potenciais elétricos cada vez menores.

Vale ainda lembrar que o vetor campo elétrico é sempre perpendicular à superfície equipotencial, e consequentemente a linha de força que o tangencia também.

${\displaystyle V_{A}=V_{B}=V_{C}=V\,}$ (ver figura ao lado)////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Potencial elétrico no eletromagnetismo

No eletromagnetismo, potencial elétrico ou potencial eletrostático é um campo equivalente à energia potencial associada a um campo elétrico estático dividida pela carga elétrica de uma partícula-teste. A unidade de medida do SI para o potencial é o volt. Apenas diferenças de potencial elétrico possuem significado físico.

O potencial elétrico gerado por uma carga pontual ${\displaystyle q\,}$ a uma distância ${\displaystyle r\,}$ é, a menos de uma constante arbitrária, dado por:

${\displaystyle \phi _{\mathbf {E} }={\frac {q}{4\pi \epsilon _{0}r}}}$

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Pontos críticos do potencial

As linhas de campo elétrico apontam na direção em que o potencial decresce. Consequentemente, num ponto onde o potencial tiver um valor máximo local, existirão linhas a apontar para fora desse ponto (nó repulsivo); o fluxo numa superfície fechada à volta desse ponto será positivo. Isso implica que na região onde o potencial é máximo deverá existir carga positiva.

Superfícies equipotenciais de um sistema de 3 cargas positivas

Num ponto onde o potencial tiver um valor mínimo local, as linhas de campo apontarão na direção desse ponto (nó atrativo). O fluxo numa superfície fechada à volta do ponto será negativo. Assim, deverá existir carga negativa nesse ponto.^[1]

Os pontos máximos e mínimos do potencial podem ser pontos onde o potencial aproxima-se de ${\displaystyle +\infty }$ ou ${\displaystyle -\infty }$, no caso de cargas pontuais, ou pontos de equilíbrio, onde as derivadas do potencial são todas nulas. Existe um terceiro tipo de ponto crítico, ponto de sela, em que o potencial é máximo em algumas direções e mínimo em outras. Portanto, em algumas direções entram linhas de campo e em outras direções saem; o fluxo numa superfície fechada à volta do ponto deverá ser nulo e, assim, nesse ponto o campo será nulo. Os pontos de sela são pontos de equilíbrio instável.^[1]

Como nos pontos máximos e mínimos do potencial há linhas de campo a sair ou entrar em todas as direções, esses pontos encontram-se dentro de superfícies equipotenciais fechadas, umas dentro das outras, aproximando-se do ponto mínimo ou máximo. Nos pontos de sela há sempre um cruzamento das superfícies equipotenciais.

Potencial e energia eletrostática

Se uma partícula com carga ${\displaystyle q}$ se deslocar entre dois pontos onde existe uma diferença de potencial ${\displaystyle \Delta V}$ a variação da sua energia potencial eletrostática será:

${\displaystyle \Delta U_{e}=q\,\Delta V}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Devido a que o campo elétrico é um campo conservativo, a energia mecânica conserva-se e a variação da energia potencial implica uma variação da energia cinética.

Quando se trata de partículas elementares com cargas da ordem de grandeza da carga elementar, costuma usar-se uma unidade de energia designada de elétrón-volt (eV), que corresponde à energia adquirida por um eletron quando se deslocar para uma região onde o potencial aumenta em 1 V. Assim, passando para o sistema internacional:

${\displaystyle 1\,\mathrm {eV} =1.6\times 10^{-19}\,\mathrm {C} \times 1\,\mathrm {V} =1.6\times 10^{-19}\,\mathrm {J} }$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Potencial e campo nos condutores

Consideremos um condutor cilíndrico e retilíneo com os dois extremos ligados aos terminais de uma bateria. Entre os extremos do condutor existirá uma diferença de potencial. Se A for o extremo que está ligado ao terminal negativo e B o extremo ligado ao terminal positivo, o potencial será maior em B do que em A: VB > VA.^[1]

As cargas de condução no condutor deslocam-se na direção do campo elétrico; no mesmo sentido do campo, se forem cargas positivas, ou no sentido oposto se forem negativas. Assim, as linhas de campo elétrico deverão ser retas paralelas ao eixo do cilindro. Portanto, o campo tem módulo E constante e segue a direção do deslocamento d s ao longo do condutor; o integral de linha que define a diferença de potencial , pode ser calculado facilmente:

${\displaystyle \int \limits _{B}^{A}E\;ds=V_{B}-V_{A}\quad \Rightarrow \quad V_{B}-V_{A}=E\;\Delta s}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde ${\displaystyle \Delta s}$ é o comprimento do condutor.^[1] Assim, o módulo do campo no condutor é igual à diferença de potencial entre os seus extremos, dividida pelo seu comprimento:

${\displaystyle E={\frac {\Delta V}{\Delta s}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

O resultado anterior também mostra que o campo aponta sempre desde o ponto com maior potencial até o ponto com menor potencial, já que para obtermos um resultado positivo, tivemos que integrar desde B até A.

Corrente e campo elétrico em dois condutores diferentes, ligados à mesma diferença de potencial

Se o condutor na figura acima for um semicondutor tipo N, as cargas de condução negativas deslocam-se no sentido oposto ao campo e, portanto, a corrente é no sentido do campo. Se o semicondutor for do tipo P, as cargas de condução positivas deslocam-se no sentido do campo e a corrente também é no sentido do campo. Consequentemente, independentemente o tipo de condutor ou semicondutor, a corrente será sempre na direção e sentido do campo elétrico, nomeadamente, desde o extremo com maior potencial para o extremo com menor potencial.^[1]

Se o condutor não for retilíneo, como no lado direito da figura, as linhas de campo já não são retas mas seguirão a direção do condutor. Isso implica que o campo vetorial ${\displaystyle {\vec {E}}}$ não é constante, mas se o condutor for homogéneo, as separação entre as linhas será sempre igual, indicando que o módulo E do campo é constante.

Potencial de uma esfera condutora

Potencial produzido por uma esfera condutora isolada.

Numa esfera condutora, as cargas distribuem-se uniformemente na superfície. Esse tipo de distribuição de carga produz um campo nulo no interior da esfera, e no exterior o campo é idêntico a que existiria se toda a carga estivesse concentrada no centro da esfera. Assim, o potencial fora da esfera deverá ser idêntico ao potencial de uma carga pontual ${\displaystyle Q}$:^[1] ${\displaystyle V={\frac {kQ}{r}}\qquad (se\quad r>a)}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

em que ${\displaystyle Q}$ é a carga total da esfera, e ${\displaystyle a}$ o seu raio.

Para que o campo seja nulo no interior da esfera, o potencial deverá ser constante nessa região. Como o potencial deve ser uma função contínua, o valor constante do potencial, dentro da esfera, deverá ser o mesmo que na superfície; nomeadamente

${\displaystyle V={\frac {kQ}{a}}\qquad (se\quad r<a)}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Dentro da esfera ${\displaystyle (r<a)}$ o campo é nulo e o potencial é constante. Fora da esfera, o potencial decresce inversamente proporcional à distância.^[1]

Potencial eletrostático

História

Em 1989, Wolfgang Paul recebeu o prêmio Nobel da física pela sua invenção da armadilha de iões que permite isolar um único ião. Com essa invenção tornou-se possível estudar um átomo isolado, e pôr a prova a física quântica, já que nas experiências anteriores estavam sempre presentes muitos átomos. O princípio de funcionamento da armadilha de iões é muito simples. Usa-se um potencial de quadrupólo, nomeadamente, um sistema em que em dois lados opostos de um quadrado há dois condutores com potenciais positivos e no outros dois lados há condutores com potenciais negativos, criando-se assim um ponto d sela no centro do quadrado.

Os iões, com carga positiva, são empurrados para o centro pelos condutores com potencial positivo, e para fora do centro pelos condutores com potencial negativo. O potencial do condutores inverte-se sucessivamente, o que faz com que após algum tempo unicamente ião que se encontra no centro permaneça nesse ponto de equilíbrio.

Potencial eletrostático e campo elétrico

A diferença de potencial entre dois pontos separados por um pequeno percurso ${\displaystyle d{\vec {r}}}$ é:

${\displaystyle dV=-{\vec {E}}\cdot d{\vec {r}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

esta equação mostra que o potencial decresce mais rapidamente na direção do campo elétrico e mantém-se constante na direção perpendicular ao campo. Em cada ponto onde o campo não for nulo, existe uma única direção em que o potencial permanece constante; o campo elétrico é perpendicular a essa direção, e aponta no sentido em que ${\displaystyle V}$ diminui (figura abaixo).

As cargas positivas deslocam-se no sentido em que o potencial decresce, e as cargas negativas deslocam-se no sentido em que o potencial aumenta.

O campo elétrico aponta na direção e sentido em que o potencial diminui mais rapidamente.

Se ${\displaystyle E_{s}}$ for a componente do campo na direção do deslocamento vetorial ${\displaystyle d{\vec {r}}}$, e ${\displaystyle d_{s}}$ for o módulo desse vetor, a equação pode ser escrita

${\displaystyle dV=-E_{s}\,ds}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Assim, a componente do campo na direção e sentido de um vetor qualquer ${\displaystyle d{\vec {r}}}$ é:

${\displaystyle E_{s}=-{\frac {dV}{d_{s}}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde ${\displaystyle dV}$ é calculado na direção do vetor ${\displaystyle d{\vec {r}}}$.

A derivada na expressão anterior é designada {derivada direccional} da função ${\displaystyle V}$, na direção definida por ${\displaystyle d{\vec {r}}}$.

Em particular, se a direção escolhida for no sentido dum dos três eixos cartesianos, ${\displaystyle E_{s}}$ será a componente do campo na direção desse eixo, e a derivada direcional será a derivada parcial em função da variável associada ao eixo:

${\displaystyle E_{x}=-{\frac {\partial V}{\partial x}}\qquad E_{y}=-{\frac {\partial V}{\partial y}}\qquad E_{z}=-{\frac {\partial V}{\partial z}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Para calcular o potencial num ponto, é costume arbitrar que o potencial seja nulo no infinito. Assim, o potencial no ponto P obtém-se a partir do integral^[1]

${\displaystyle V=-\int _{\infty }^{\mathrm {P} }{\vec {E}}\cdot d{\vec {r}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

As três componentes cartesianas do campo não podem ser quaisquer três funções da posição, já que, a partir das equações das derivadas conclui-se que:

${\displaystyle {\frac {\partial E_{x}}{\partial y}}={\frac {\partial E_{y}}{\partial x}}\qquad {\frac {\partial E_{x}}{\partial z}}={\frac {\partial E_{z}}{\partial x}}\qquad {\frac {\partial E_{y}}{\partial z}}={\frac {\partial E_{z}}{\partial y}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

essas são as condições necessárias e suficientes para garantir que o campo seja conservativo. A matriz jacobiana do campo, em função da posição, é:^[1] ${\displaystyle {\begin{bmatrix}{\frac {\displaystyle \partial E_{x}}{\displaystyle \partial x}}&{\frac {\displaystyle \partial E_{x}}{\displaystyle \partial y}}&{\frac {\displaystyle \partial E_{x}}{\displaystyle \partial z}}\\[12pt]{\frac {\displaystyle \partial E_{y}}{\displaystyle \partial x}}&{\frac {\displaystyle \partial E_{y}}{\displaystyle \partial y}}&{\frac {\displaystyle \partial E_{y}}{\displaystyle \partial z}}\\[12pt]{\frac {\displaystyle \partial E_{z}}{\displaystyle \partial x}}&{\frac {\displaystyle \partial E_{z}}{\displaystyle \partial y}}&{\frac {\displaystyle \partial E_{z}}{\displaystyle \partial z}}\end{bmatrix}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Devido às condições apresentadas acima da matriz, essa matriz é simétrica e, portanto, deverá ter unicamente valores próprios reais. Consequentemente, no espaço da posição, os pontos de equilíbrio do campo elétrico podem ser ou pontos de sela ou nós, mas nunca centros ou focos. No espaço de fase, como o sistema é conservativo, os pontos de equilíbrio podem ser pontos de sela ou centros.^[1]

Potencial devido a cargas pontuais

Em duas dimensões, o campo elétrico produzido por um sistema de ${\displaystyle n}$ cargas pontuais ${\displaystyle q_{1}}$, ${\displaystyle q-2}$, ..., ${\displaystyle q_{n}}$, é dado pela equação do Campo elétrico produzido por cargas pontuais.

O potencial é a função de ${\displaystyle x}$e ${\displaystyle y}$com derivadas parciais iguais às duas componentes do campo. Assim, o potencial é:

${\displaystyle V=\sum _{i=1}^{n}{\frac {k\,q_{i}}{\sqrt {(x-x_{i})^{2}+(y-y_{i})^{2}}}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Onde ${\displaystyle x_{i}}$ e ${\displaystyle y_{i}}$ são as coordenadas da posição da partícula ${\displaystyle i}$.<^[1]

Variáveis vetoriais

As variáveis (vetoriais) de estado de uma partícula, são a sua posição ${\displaystyle {\vec {r}}}$ e a velocidade ${\displaystyle {\vec {v}}}$ o espaço de fase tem seis dimensões: (x, y, z, vx , vy , vz).^[1] Uma partícula com massa m e carga q, numa região onde exista um campo gravítico ${\displaystyle {\vec {g}}}$ e um campo elétrico ${\displaystyle {\vec {E}}}$ sofre uma força resultante ${\displaystyle m{\vec {g}}+q{\vec {E}}}$ . As suas equações de movimento são:

${\displaystyle {\frac {d{\vec {v}}}{dt}}={\vec {g}}+{\frac {q}{m}}{\vec {E}}\quad \quad \quad \quad \quad \quad {\frac {d{\vec {r}}}{dt}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

em que os campos ${\displaystyle {\vec {g}}}$ e ${\displaystyle {\vec {E}}}$ são funções que dependem da posição ${\displaystyle {\vec {r}}}$. Essas duas equações podem ser combinadas para eliminar o tempo e obter a relação entre a posição e a velocidade:

${\displaystyle {\vec {v}}.d{\vec {v}}={\Big (}{\vec {g}}+{\frac {q}{m}}{\vec {E}}{\Big )}.d{\vec {r}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

As soluções da equação acima são as trajetórias no espaço de fase,${\displaystyle ({\vec {r}},{\vec {v}})}$ Integrando os dois lados da equação, desde um ponto inicial ${\displaystyle ({\vec {r}}_{0},{\vec {v}}_{0})}$ até um ponto final ${\displaystyle ({\vec {r}},{\vec {v}})}$ no espaço de fase e multiplicando pela massa m, obtém-se:

${\displaystyle {\frac {1}{2}}mv^{2}-{\frac {1}{2}}mv_{0}^{2}=m\;\int \limits _{{\vec {r}}_{0}}^{\vec {r}}{\vec {g}}.d{\vec {r}}+q\;\int \limits _{{\vec {r}}_{0}}^{\vec {r}}{\vec {E}}.d{\vec {r}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

A expressão no lado esquerdo é o aumento da energia cinética, e a expressão no lado direito é o trabalho realizado pelas forças gravítica e elétrica.

Num campo gravítico uniforme,${\displaystyle {\vec {g}}=-g{\vec {e}}_{y}}$ o integral do campo gravítico não depende do percurso de integração, mas apenas das posições inicial e final,

${\displaystyle \int \limits _{{\vec {r}}_{0}}^{\vec {r}}-g{\vec {e}}_{y}.d{\vec {r}}=g(y_{0}-y)}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

e a função ${\displaystyle U_{g}=m\;g\;y}$ define a energia potencial gravítica. Devido a que o campo gravítico é conservativo, qualquer outro campo gravítico mais complicado também conduz a umintegral de linha que não depende do percurso usado e é possível associar a cada campo gravítico uma função escalar que multiplicada pela massa dá a energia potencial.^[1]

No caso do campo elétrico a situação é análoga; os campo eletrostáticos (campos elétricos que não variam com o tempo) são sempre conservativos e, portanto, para cada campo eletrostático existe uma função escalar V (x,y,z) que permite calcular o integral de linha do campo sem ser preciso saber o percurso de integração:

${\displaystyle \int \limits _{{\vec {r}}_{0}}^{\vec {r}}{\vec {E}}.d{\vec {r}}=V(x_{0},y_{0},z_{0})-V(x,y,z)}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

A função V designa-se potencial eletrostático e a energia potencial eletrostática é:

${\displaystyle U_{e}=qV}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Em função das energias potenciais gravítica eletrostática, a equação de movimento é a lei da conservação da energia mecânica:

${\displaystyle {\frac {1}{2}}mv^{2}+U_{e}+U_{g}={\frac {1}{2}}mv_{0}^{2}+U_{e}0+U_{g}0}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

No sistema internacional de unidades, a unidade do potencial elétrico V é o joule sobre coulomb, unidade essa que é designada de volt e denota-se com a letra V:

${\displaystyle 1\;V=1\;J/C}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

A unidade SI do campo elétrico é N/C, que pode ser escrito como J/(m.C); consequentemente, N/C é equivalente a V/m e o campo elétrico pode ser interpretado como a diferença de potencial por unidade de comprimento.

É de salientar que, devido a que a carga q pode ser positiva ou negativa, a energia eletrostática ${\displaystyle U_{e}}$ de uma partícula com carga negativa será maior nos pontos onde o potencial for menor, enquanto que as partículas com carga positiva terão maior energia nos pontos. Consequentemente, a equação que explica a função das energias potenciais gravíticas eletrostáticas, implica que, dentro de um campo elétrico, as partículas com carga positiva são aceleradas para a região com menor potencial e as partículas com carga negativa são aceleradas para a região com maior potencial.^[1]

A lei de conservação da energia mecânica só é válida para cargas que se deslocam no vácuo. As cargas que se deslocam dentro de um material condutor, como um metal, ou dentro de um isolador, como o ar, estão sujeitas a forças dissipativas que fazem diminuir rapidamente a energia mecânica, até a carga ficar em repouso, onde o potencial for maior.

Eletromagnetismo
Representação do vetor campo elétrico de uma onda eletromagnética circularmente polarizada.
Eletrostática[Expandir]
História[Expandir]
Magnetostática[Expandir]
Eletrodinâmica[Expandir]
Circuitos elétricos[Expandir]
Físicos[Expandir]
v d e

Um campo elétrico (AO 1945: campo eléctrico) é o campo de força provocado pela ação de cargas elétricas, (elétrons, prótons ou íons) ou por sistemas delas. Cargas elétricas colocadas num campo elétrico estão sujeitas à ação de forças elétricas, de atração e repulsão.

A equação usada para se calcular a intensidade do vetor campo elétrico (E) é dada pela relação entre a força elétrica (F) e a carga de prova (q):

${\displaystyle \mathbf {E} ={\frac {\mathbf {F} }{|q|}}}$

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

O campo elétrico pode ser definido pelo negativo do gradiente do potencial elétrico:

${\displaystyle {\vec {E}}=-{\vec {\nabla }}V}$

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Unidade no Sistema Internacional de Unidades:

${\displaystyle [E]={\frac {N}{C}}\qquad (N/C)}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Onde N é a unidade de força (Newton) e C a unidade de carga (Coulomb).

Índice

• 1História
• 2Vetor campo elétrico
• 3Campo elétrico devido a uma carga elétrica
• 4Campo elétrico uniforme
• 5Linhas de força
• 6Campo elétrico gerado por uma esfera oca condutora
• 7Campo elétrico produzido por cargas pontuais
• 8Lei de Gauss no campo
• 9Campo de um plano
• 10Campo de um fio retilíneo
• 11Campo de uma esfera condutora
• 12Campo elétrico induzido
• 13Propriedades das linhas de campo elétrico
• 14Ver também
• 15Referências
• 16Bibliografia
• 17Ligações externas

História

Os estudos a respeito da eletricidade estática, criadora dos campos elétricos, remontam ao filósofo grego Tales de Mileto no século VI a.C.. O filósofo e estudioso da natureza descreveu o fenômeno que consiste em uma barra de âmbar (seiva petrificada) que atrai pequenos objetos depois de atritada com uma pele de coelho. No cotidiano, é o mesmo que esfregar uma caneta de plástico (material isolante) contra um pano ou o próprio cabelo. Em ambas as situações, o objeto fica eletricamente carregado.

A explicação da força entre partículas através da existência de um campo vem desde a época em que foi desenvolvida a teoria da gravitação universal. A dificuldade em aceitar que uma partícula possa afetar outra partícula distante, sem existir nenhum contato entre elas, foi ultrapassada na física clássica com o conceito do campo de força. No caso da força eletrostática, o campo mediador que transmite a força eletrostática foi designado por éter; a luz seria uma onda que se propaga nesse éter lumínico. No século XIX foram realizadas várias experiências para detectar a presença do éter, sem nenhum sucesso.

No fim do século chegou-se à conclusão de que não existe tal éter. No entanto, o campo elétrico tem existência física, no sentido de que transporta energia e que pode subsistir até após desaparecerem as cargas que o produzem. Na física quântica a interação elétrica é explicada como uma troca de partículas mediadoras da força, que são as mesmas partículas da luz, os fotões. Cada carga lança alguns fotões que são absorvidos pela outra carga; no entanto, neste artigo falaremos sobre a teoria clássica do campo, onde o campo é como um fluido invisível que arrasta as cargas elétricas.

Vetor campo elétrico

Campo elétrico gerado pela carga Q

O campo elétrico em um ponto é uma grandeza vetorial, portanto é representado por um vetor. Para verificarmos a sua presença neste ponto, colocamos neste uma carga de prova positiva. Se esta ficar sujeita a uma força eletrostática, dizemos que a região em que a carga se encontra está sujeita a um campo elétrico. O vetor campo elétrico tem sempre a mesma direção da força a que a carga está sujeita e, no caso da carga ser positiva, o mesmo sentido. Se negativa o oposto. O módulo é calculado da seguinte forma:

${\displaystyle {\vec {E}}={\frac {\vec {F}}{q}}}$ onde, caso a carga seja puntiforme, ${\displaystyle |{\vec {F}}|={\frac {k.|Q|.|q|}{d^{2}}}}$ (lei de Coulomb)

O módulo do vetor campo elétrico pode ser definido por:

${\displaystyle E={\frac {F}{q}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Substituindo ${\displaystyle F\Rightarrow E={\frac {k.|Q|}{d^{2}}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

${\displaystyle k={\frac {1}{4\pi \varepsilon _{0}}}=8,99\times 10^{9}}$, é a constante de Coulomb ou constante eletrostática do meio e ${\displaystyle \varepsilon _{0}=8,85\times 10^{-12}}$ é a constante de permissividade do vácuo.^[1][2]

Nota-se, por essa expressão, que o campo elétrico gerado por uma carga em um ponto é diretamente proporcional ao seu valor e inversamente proporcional ao quadrado da distância.

Campo elétrico devido a uma carga elétrica

O campo elétrico sempre "nasce" nas cargas positivas (vetor) e "morre" nas cargas negativas. Isso explica o sentido do vetor mencionado acima. Quando duas cargas positivas são colocadas próximas uma da outra, o campo elétrico é de afastamento, gerando uma região entre as duas cargas isenta de campo elétrico. O mesmo ocorre para cargas negativas, com a diferença de o campo elétrico ser de aproximação. Já quando são colocadas próximas uma carga positiva e uma negativa, o campo "nasce" na primeira, e "morre" na segunda.

Na equação: F = k.Q.q/d² , k é a constante eletrostática do meio e não a constante dielétrica.

Campo elétrico uniforme

É definido como uma região em que todos os pontos possuem o mesmo vetor campo elétrico em módulo, direção e sentido. Sendo assim, as linhas de força são paralelas e equidistantes.

Para produzir um campo com essas características, basta utilizar duas placas planas e paralelas eletrizadas com cargas de mesmo módulo e sinais opostos. Um capacitor plano de placas paralelas pode ser citado como exemplo de criador de um campo elétrico uniforme.

Linhas de força

As cargas de prova positivas encontram-se em movimento dentro de um campo elétrico. A partir da trajetória dessas cargas, traçam-se linhas que são denominadas linhas de força, que têm as seguintes propriedades:

1. Saem de cargas positivas e entram nas cargas negativas;
2. As linhas são tangenciadas pelo campo elétrico;
3. Duas linhas de força nunca se cruzam;
4. A intensidade do campo elétrico é proporcional à concentração das linhas de força.

Campo elétrico gerado por uma esfera oca condutora

Quando uma esfera está eletrizada, as cargas em excesso repelem-se mutuamente e por isso migram para a superfície externa da esfera, atingindo o equilíbrio eletrostático. Assim, o campo elétrico dentro da esfera (em equilíbrio eletrostático) é nulo.

1. ${\displaystyle E_{i}=0\quad }$ (No interior da Esfera)
2. ${\displaystyle E={\frac {k\cdot Q}{R^{2}}}}$ (superfície exterior próxima da esfera)////

   TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

3. ${\displaystyle E={\frac {k\cdot Q}{(R+d)^{2}}}}$ (distante da esfera), onde R é o raio da esfera.////

   TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Campo elétrico produzido por cargas pontuais

A equação para o módulo do campo produzido por uma carga pontual pode ser escrita de forma vetorial.^[3] Se a carga Q estiver na origem, o resultado obtido é:

${\displaystyle {\vec {E}}={\frac {k\,Q}{r^{2}}}{\vec {e}}_{r}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Campos produzidos por duas cargas de 4 nC e 9 nC em alguns pontos (lado esquerdo) e o campo resultante nesses pontos (lado direito)

sendo r a distância até a origem, e ${\displaystyle {\vec {e}}_{r}}$ o vetor unitário que aponta na direção radial, afastando-se da carga.

Se a carga for negativa, a equação anterior continua válida, dando um vetor que aponta no sentido oposto de ${\displaystyle {\vec {e}}_{r}}$ (campo atrativo).

O vetor unitário ${\displaystyle {\vec {e}}_{r}}$ calcula-se dividindo o vetor posição ${\displaystyle {\vec {r}}}$ pelo seu módulo, r.

Se a carga não estiver na origem mas numa posição ${\displaystyle {\vec {r}}_{1}}$ a equação acima pode ser generalizada facilmente, dando o resultado:^[3]

${\displaystyle {\vec {E}}={\frac {k\,Q({\vec {r}}-{\vec {r}}_{1})}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

O campo produzido por um sistema de cargas pontuais obtém-se somando vetorialmente os campos produzidos por cada uma das cargas.

Por exemplo o lado esquerdo na figura acima à direita mostra os campos produzidos por duas cargas pontuais de 4 nC e 9 nC em alguns pontos. O lado direito mostra o campo resultante, obtido somando vetorialmente os dois campos.

A equação anterior pode ser generalizada para um sistema de n cargas pontuais. Vamos escrever a equação explicitamente, em função das coordenadas cartesianas no plano xy (a generalização para o espaço xyz será evidente).

Se as cargas ${\displaystyle q_{1},q_{2},...,q_{n}}$estiverem nos pontos ${\displaystyle (x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n}),}$ , o resultado é:

${\displaystyle {\vec {E}}=\sum _{i=1}^{n}{\Bigg [}{\frac {k\,q_{i}\,(x-x_{i})}{[(x-x_{i})^{2}+(y-y_{i})^{2}]^{3/2}}}{\Bigg ]}\,{\vec {e}}_{x}+\sum _{i=1}^{n}{\Bigg [}{\frac {k\,q_{i}\,(y-y_{i})}{[(x-x_{i})^{2}+(y-y_{i})^{2}]^{3/2}}}{\Bigg ]}\,{\vec {e}}_{y}}$

////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Lei de Gauss no campo

O fluxo elétrico através da superfície fechada depende unicamente da carga interna, neste caso q1 + q2.

O fluxo elétrico produzido por várias cargas pontuais, através de uma superfície fechada, é igual à soma dos fluxos produzidos por cada uma das cargas. O fluxo das cargas pontuais que estejam fora da superfície fechada será nulo, e o fluxo das cargas que estejam dentro da superfície será ${\displaystyle 4\,\pi \,k}$ vezes o valor da carga. Por exemplo, no caso da figura abaixo, unicamente as duas cargas ${\displaystyle q_{1}}$ e ${\displaystyle q_{2}}$ produzem fluxo, porque a carga ${\displaystyle q_{3}}$ encontra-se fora da superfície.

O fluxo total é:

${\displaystyle \Phi _{\mathrm {e} }=4\,\pi \,k\left(q_{1}+q_{2}\right)}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

O resultado do exemplo da figura acima pode ser generalizado para qualquer sistema de cargas e qualquer superfície fechada, e é designado de Lei de Gauss:

O fluxo através de qualquer superfície fechada é igual à carga total no interior da superfície, multiplicada por ${\displaystyle 4\,\pi \,k}$

Em termos matemáticos, a lei de Gauss determina que o fluxo elétrico através de qualquer superfície fechada é:

${\displaystyle {\Phi _{\mathrm {e} }=4\,\pi \,k\,q_{\text{int}}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Se a carga total no interior for positiva, o fluxo será positivo, indicando que há linhas de campo a saírem da superfície. Se a carga interna total for negativa, o fluxo é negativo porque há linhas de campo a entrar na superfície.

O fluxo elétrico total à volta de uma carga pontual é diretamente proporcional à carga. Em alguns casos é possível desenhar um número de linhas de campo proporcional à carga, para dar uma ideia mais aproximada do valor do fluxo em diferentes regiões; por exemplo, na figura anterior foram desenhadas 8 linhas de campo a saírem da carga de 4 nC, e 18 linhas a saírem da carga de 9 nC.

A lei de Gauss é muito útil para calcular campos elétricos de sistemas com simetria.

Campo de um plano

Cilindro imaginário usado para calcular o campo do plano.

Consideremos um plano, com carga distribuída uniformemente. Visto de lado, o plano aparece como um segmento de reta, e as linhas de campo serão semelhantes às linhas representadas no lado direito da figura ao lado.^[3]

Nas regiões perto do centro do plano, as linhas de campo são aproximadamente paralelas entre si. Quanto maior for o plano, maior será a região onde as linhas são aproximadamente paralelas..^[3]

No caso idealizado de um plano infinito, as linhas serão completamente paralelas e equidistantes, já que a aparência do plano seria a mesma em qualquer ponto.

Para calcular o campo elétrico usando a lei de Gauss, imaginamos um cilindro com as tampas paralelas ao plano, como se mostra na figura.

Nas paredes laterais do cilindro não existe fluxo elétrico, porque o campo é paralelo à superfície. Em cada uma das tampas circulares do cilindro, o campo é perpendicular e, com módulo constante, devido a que todos os pontos na tampa estão à mesma distância do plano.

Assim, o fluxo em cada uma das tampas do cilindro é ,${\displaystyle A\,E}$ , em que A é a área da tampa, e o fluxo total através do cilindro é:^[3]

${\displaystyle \Phi _{\mathrm {e} }=2\,A\,E}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

De acordo com a lei de Gauss, esse fluxo também deverá ser igual a:

${\displaystyle \Phi _{\mathrm {e} }=4\,\pi \,k\,Q}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Onde Q é a carga na parte do plano que está dentro do cilindro. Igualando as duas últimas equações obtemos o módulo do campo:

${\displaystyle E_{\mathrm {plano} }=2\,\pi \,k\,\sigma }$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Em que ${\displaystyle \sigma }$ é a carga superficial; nomeadamente, carga por unidade de área:

${\displaystyle \sigma ={\frac {Q}{A}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Campo de um fio retilíneo

Linhas de campo de um cilindro com carga distribuída uniformemente, e superfície usada para calcular o campo.

Consideremos um fio retilíneo, muito comprido, com carga distribuída uniformemente. As linhas de campo deverão ser nas direções radiais. Imaginemos uma superfície fechada que é um cilindro de raio R e altura L, com eixo sobre o fio, como mostra a figura abaixo.^[3]

Nas tampas circulares do cilindro o fluxo é nulo, porque o campo é paralelo à superfície; na parede lateral do cilindro, o campo é perpendicular e com módulo constante.^[3]

${\displaystyle \Phi _{\mathrm {e} }=2\,\pi \,R\,L\,E}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde E é o módulo do campo à distância R do fio. De acordo com a lei de Gauss, esse fluxo deverá ser também igual a:

${\displaystyle \Phi _{\mathrm {e} }=4\,\pi \,k\,Q}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

onde Q é a carga do fio que está dentro do cilindro S. Igualando as duas equações anteriores, obtemos o módulo do campo:

${\displaystyle {E_{\text{fio}}={\frac {2\,k\,\lambda }{R}}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

em que ${\displaystyle \lambda }$ é a carga linear (carga por unidade de comprimento): ${\displaystyle \lambda =Q/L}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Campo de uma esfera condutora

Numa esfera condutora, com carga Q e raio a, a força repulsiva entre as cargas do mesmo sinal, faz com que as cargas se distribuam em forma uniforme, na superfície da esfera. Existe assim simetria esférica, e as linhas de campo deverão apontar na direção radial..^[3]

Para calcular o campo, imaginamos uma esfera de raio r,concêntrica com a esfera condutora. .^[3] Na superfície dessa esfera, o campo será perpendicular, e com módulo constante E; consequentemente o fluxo será:

${\displaystyle \Phi _{\mathrm {e} }=4\,\pi \,r^{2}\,E}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Segundo a lei de Gauss, o fluxo através da esfera de raio r será nulo, se ${\displaystyle r<a}$, ou igual a ${\displaystyle 4\,\pi \,k\,Q}$ se ${\displaystyle r>a}$. Portanto, o campo elétrico é nulo, no interior da esfera.

Fora da esfera o campo é:

${\displaystyle E={\frac {k\,Q}{r^{2}}}}$////

TEORIA GRACELI GERAL E UNIFICATÓRIA do INFINITO-DIMENSIONAL.

Que é idêntico ao campo produzido por uma carga Q concentrada no centro da esfera.<.^[3]

Campo elétrico induzido

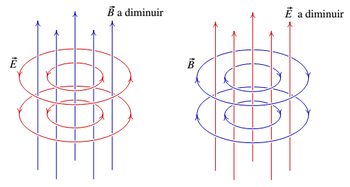
Um campo magnético variável no tempo induz um campo elétrico, e um campo elétrico variável induz um campo magnético.

O campo elétrico induzido é proporcional à derivada do fluxo magnético, e o campo magnético induzido é proporcional à derivada do fluxo elétrico. Quando um campo é uniforme, o fluxo através de uma superfície é maior se a superfície for perpendicular ao campo; isso implica que o campo induzido é perpendicular ao campo variável.^[3]

Campo elétrico induzido por um campo magnético uniforme mas variável(esquerda) e campo magnético induzido por um campo elétrico uniforme ,mas variável (direita).

A figura ao lado mostra o campo elétrico induzido por um campo magnético uniforme mas variável, e o campo magnético induzido por um campo elétrico uniforme e variável. No primeiro caso, devido ao sinal negativo , o campo elétrico induzido é no sentido oposto ao obtido com a regra da mão direita em relação à derivada do campo magnético; como o campo magnético está a diminuir, a derivada do campo aponta para baixo e a regra da mão direita indica rotação no sentido horário; portanto, as linhas do campo induzido estão orientadas no sentido anti-horário.

O sinal positivo do último termo implica que as linhas do campo magnético induzido seguem a regra da mão direita em relação ao aumento do campo elétrico. No caso do campo elétrico variável no lado direito da figura , como o campo está a diminuir, a derivada do campo elétrico aponta para baixo, e a regra da mão direita indica que o campo magnético induzido é no sentido horário.^[3]

Propriedades das linhas de campo elétrico

Linhas de campo elétrico perto de uma carga negativa (esquerda) e de uma carga positiva (direita).

O campo elétrico pode ser representado por vetores que indicam o valor do campo em vários pontos do espaço, como foi feito na figura acima. O problema com essa representação é que o campo varia rapidamente com a distância, o que faz com que o vetor seja muito grande em alguns pontos e muito pequeno em outros pontos.

A representação usando linhas de campo é mais conveniente. As linhas de campo seguem a direção do campo. Em cada ponto numa dessas curvas, o campo é tangente à curva e no sentido indicado pelas setas.

As linhas de campo elétrico têm várias propriedades:

• Perto de uma carga pontual positiva há linhas a sair em todas as direções e perto de uma carga negativa há linhas a entrarem em todas as direções;

• Duas linhas de campo nunca se podem cruzar; no ponto de cruzamento o campo teria duas direções diferentes, que não é possível;

• A matriz jacobiana correspondente ao campo elétrico é sempre simétrica. Isso implica que os valores próprios dessa matriz serão sempre reais e nunca complexos. Assim, os únicos pontos de equilíbrio que podem existir num campo elétrico são nós e pontos de sela.

Campo elétrico criado por um dipolo (esquerda) e por um sistema de 7 cargas no segmento de reta entre x = - 3 e x = 3.

Um nó pode ser atrativo ou repulsivo. Se for atrativo, será um ponto onde existe uma carga pontual negativa; se for repulsivo, será um ponto onde existe uma carga pontual positiva. Os pontos de sela são pontos onde o campo é nulo, mas não existe nenhuma carga nesse ponto.

Outro exemplo são as linhas de campo de um dipolo elétrico, formado por duas cargas iguais mas de sinais opostos. Se admitirmos que as duas cargas estão localizadas nos pontos ( 1, 0) e (1, 0), o campo desenha-se assim:

O resultado aparece no lado esquerdo acima à direita

Uma distribuição contínua de cargas pode ser aproximada por uma série de cargas pontuais. Por exemplo, se existirem cargas distribuídas uniformemente no segmento do eixo dos x entre x = - 3 e x = 3, podemos admitir um sistema de cargas pontuais, equidistantes, sobre o segmento entre x = - 3 e x = 3.

Com 7 cargas pontuais, o gráfico obtido é apresentado no lado direito da figura ao lado.